Selecting Mailboxes for Migration

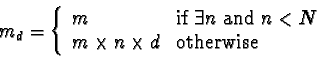
A metric is calculated for each user and a total is generated for each server. It is advisable, to measure this metric over a reasonable period of time, such as a week as individual's mail usage varies from day to day and in particular, usage on weekends is quite different to that on weekdays. It is quite undesirable, to be in a situation where mail servers do mass migrations, when the weekend begins and ends, as the overhead involved in migration is non-trivial. Once the metric has been measured, mailboxes need to be migrated to or from the server, if the total for the server is below or above the mean server total by more than a tolerance. The tolerance is designed to avoid migration as the result of fluctuations in usage by users. A tolerance of 5% is a good starting point, though may prove a little generous on a well tuned system.

When performing migrations, it is preferable to perform as few migrations as possible, to minimise changes that need to be propagated throughout the system. For this reason, it makes sense to move users who have a large metric, as this has the same effect as moving a larger number of users with a smaller metric.

Servers that are overloaded and hence, require users to be migrated to another server, arrange all users in order of their metric into a list. Users whose removal from the server would cause the server's total metric to fall below the mean are omitted from the list. For each user in the list, a decayed metric is calculated as follows;

Let m be the user's metric.
Let N be the number of days that a migration is remembered for.
Let n be the number of days since the user's mailbox was migrated.
Let m_d be the user's decayed metric.
Let d be the rate of decay.

$$m_{d} = \left\{ \begin{array}{ll} m & \mbox{if $\exists n$\s... ...\times n \times d & \mbox{otherwise} \\ \end{array} \right.$$

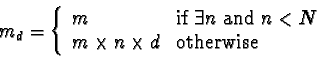
If a N=10, that is migrations are remembered for 10 days and the user's mailbox was migrated yesterday so n=1. If d=0.1 then $m_{d} = m \times 1 \times 0.1 = 0.1n$. The decayed metric is used to determine the probability of a mailbox being migrated. The reason for this, is to avoid a situation where the same mailbox is migrated over and over again, as may occur is a mailbox has a particularly large metric.

The ordered lists from each overloaded server are then merged and the most underloaded server then truncates the list, such that only users whose metric would not cause the server to become overloaded are included in the list. This leaves a list of users who can be migrated to the underloaded server in question without overloading the server and can be removed from the server that currently handles their mail without causing that server to become underloaded. If this list is empty then no migration takes place, otherwise a user is chosen using the decayed metric as follows;

Imagine a dart board divided up into areas for each user. This is now modified, such that the area for each user corresponds to its decayed metric, plus a small amount to ensure that all users have some area on the dart board. A dart is thrown in such a way that it has equal probability of hitting any part of the dart board, which though, practically impossible, will do for this analogy. The user that the dart lands on is our selected user.